|
(* Copyright (C)2024 Sasan Ardalan *)
(* This program is free software:you can redistribute it and/or modify *)
(* it under the terms of the GNU General Public License as published by*)
(* the Free Software Foundation,either version 3 of the License,or *)
(*(at your option) any later version.This program is distributed *)
(* in the hope that it will be useful,but WITHOUT ANY WARRANTY *)
(* without even the implied warranty of *)
(* MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE.See the *)
(* GNU General Public License for more details.You should have *)
(* received a copy of the GNU General Public License *)
(* along with this program.If not,see. *)
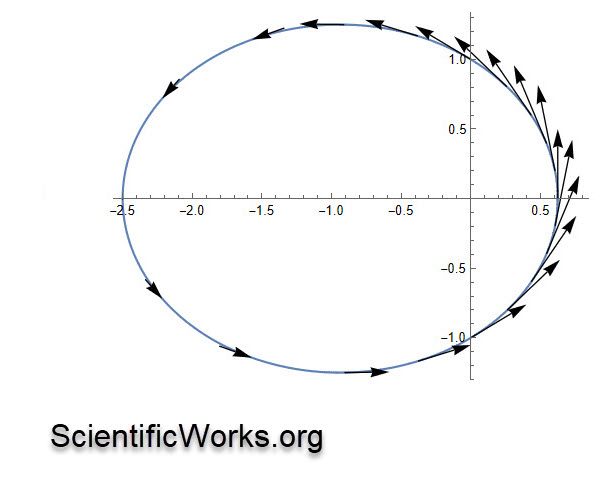
(* Velocity Vector for Elliptic Orbits *)
(* Orbital Mechanics *)
(* Author: Sasan Ardalan *)
(* ScientificWorks.org *)
(* Date: September 10, 2024 *)
p = 1.0
e = 0.6
f[theta_] := p/(1 + e*Cos[theta])
PolarPlot[f[theta], {theta, 0, 2*Pi}]
dyDivdx[theta_] := (
e*(Sin[theta])^2 +
f[theta]*Cos[theta]*(1 + e*Cos[theta])^2)/(e*Sin[theta]*
Cos[theta] - f[theta]*Sin[theta]*(1 + e*Cos[theta])^2)
arrows = {}
delTheta = 0.1*Pi
theta = 0;
For[i = 0, i < 20, i++,
theta = theta + delTheta;
(*theta=Pi*(0.1); *)
(* Print["Theta:",theta]; *)
m = dyDivdx[theta];
(* Print["Slope m:",m]; *)
r = f[theta];
x0 = r*Cos[theta];
y0 = r*Sin[theta];
(* Print["x0=",x0," y0=", y0]; *)
n = y0 - m*x0;
ftan[x_] := m*x + n;
x = x0;
yy = ftan[x0];
(* Print["x0==",x0," yy=", y0]; *)
(*Plot[ftan[x],{x,-4,2}]*)
lenF = 0.4;
ra = 1/(1 + e);
rb = 1/(1 - e);
a = (ra + rb)/2;
(* Print["a first=",a]*)
a = 1/(1 - e^2);
(* Print["a=",a]; *)
velocity = Sqrt[(2*a - r)/(r*a)];
(*Print ["Velocity =",velocity]; *)
deltax = lenF/Sqrt[1 + m^2]*velocity;
x11 = If[m < 0, x0 - deltax, x0];
x22 = If[m < 0, x0, x0 + deltax];
x1 = x11;
x2 = x22;
(*Print["x0=",x0," x1=",x1," x2=",x2];*)
arrows =
If[theta > Pi,
Append[arrows, Arrow[{{x1, ftan[x1]}, {x2, ftan[x2]} }]],
Append[arrows, Arrow[{{x2, ftan[x2]}, {x1, ftan[x1]} }]]]
]
Show[PolarPlot[f[theta], {theta, 0, 2*Pi}], Graphics[arrows]]
|


 Link
Link .
.